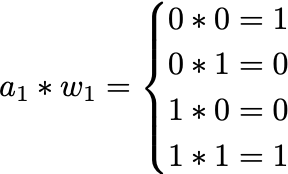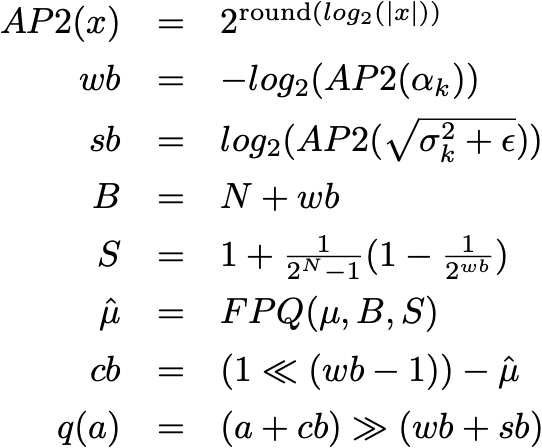12倍端到端加速，陈天奇创业公司OctoML提出克服二值网络瓶颈新方法

去年，TVM 开发团队陈天奇等人创建了 OctoML 公司，旨在「让机器学习可以部署在所有硬件上」。前段时间，该公司推出了第一个软件即服务产品Octimizer，可以帮助开发者更方便、快捷地将 ML 模型部署到设备上。近日，该公司官方博客又介绍了一种快速端到端二值神经网络——Riptide，使用 TVM 进行优化时可以实现最高 12 倍的端到端加速。该公司机器学习系统工程师 Josh Fromm 在博客中介绍了 Riptide 的细节。

Riptide 是一种新的模型量化方法，可以将模型量化至 1、2 位。研究团队今年三月在 MLSys 上介绍了 Riptide，这篇文章主要讲一下为什么要构建 Riptide，并快速了解它的幕后工作原理。团队计划来年将 Automatic ultra low-bit 功能添加到 Octomizer 中。在此之前，读者可以使用开源 Riptide 项目和 MLSys 论文中的信息来进行模型优化。

• 论文链接：https://proceedings.mlsys.org/static/paper_files/mlsys/2020/155-Paper.pdf
• GitHub 项目：https://github.com/jwfromm/Riptide

动机及背景

机器学习发展迅速。几乎每个月，那些优秀的新模型都会大大提高一些视觉或语言任务方面的 SOTA。这些改进一部分是由新的算法和架构创新所推动的，但对于深度学习任务来说，不断扩展的算力和内存也使其取得了重大进展。

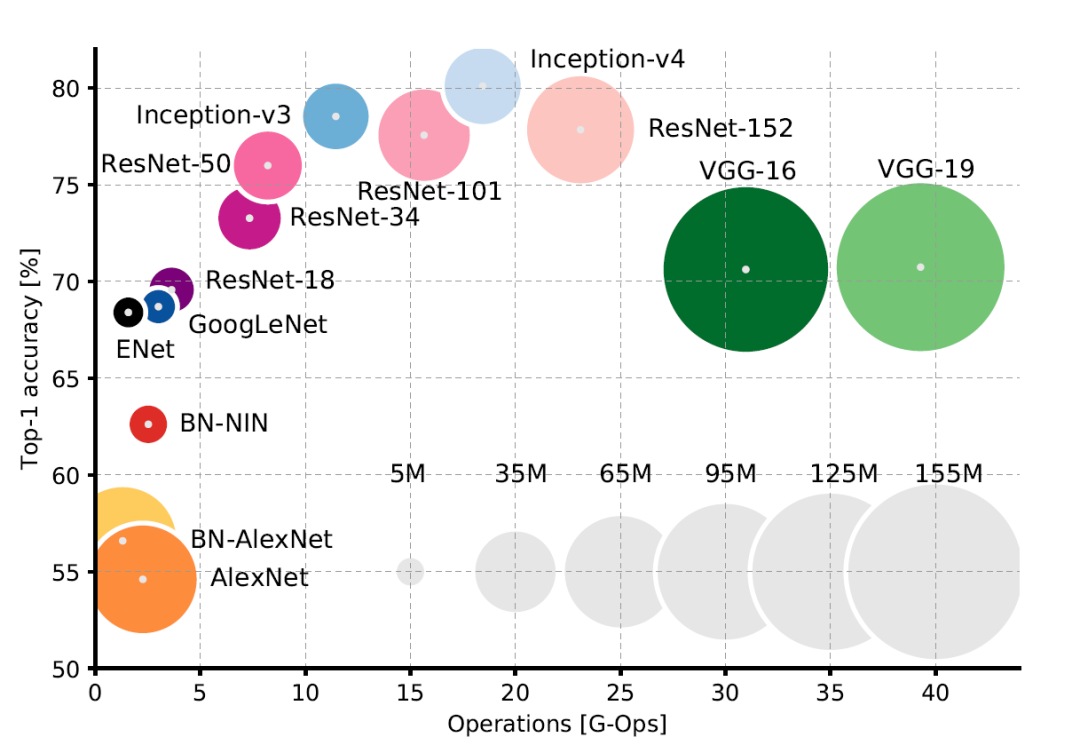
随着 ML 准确率的提升，模型所需要的算力和内存也不断增加。

早在 2016 年，我们就可以看出模型大小和准确率之间的关系了。当下，许多 SOTA 模型只能在最新的 NVIDIA GPU（或 GPU 集群）上才能有效运行。而许多用户无法花费数千美元在高端 GPU 上，所以就限制了模型部署的范围。

由于各类网络可能只需要训练一次，开发人员也许可以证明这种训练费用是合理的、有效的。但是，一旦模型进行了部署，将长时间被大量用户不断运行。要以这种规模部署最新的模型，通常需要将输入数据流传输到云上，并将预测返回到用户设备。现在许多应用程序都依赖这种方法，但它有一些缺点，体现在网络连接性、延迟、隐私问题以及庞大复杂的基础架构上。

为了避免这些缺点，许多团队探索如何在低成本的终端用户硬件（如手机或 IoT 设备）上直接运行最新模型。这是一个巨大的挑战，因为此类设备没有足够的算力或内存。例如，树莓派 3 比 NVIDIA Titan GPU 慢了大约 4000 倍。

为了使高精度模型适应此类平台，最近的研究方向已经开始探索如何使这类网络运行更快，同时占用更少的内存。从较高的层面来说，这些技术遵循两种策略：体系架构优化和近似优化。架构优化涉及寻找连接层的新方法，以减少延迟或提高参数有效性。MobileNet 和 SqueezeNet 是两个以移动端为重点的体系架构。与创建新的移动设备友好型模型相反，近似优化旨通过加快运算速度提高现有模型的速度，同时保持足够的准确率。

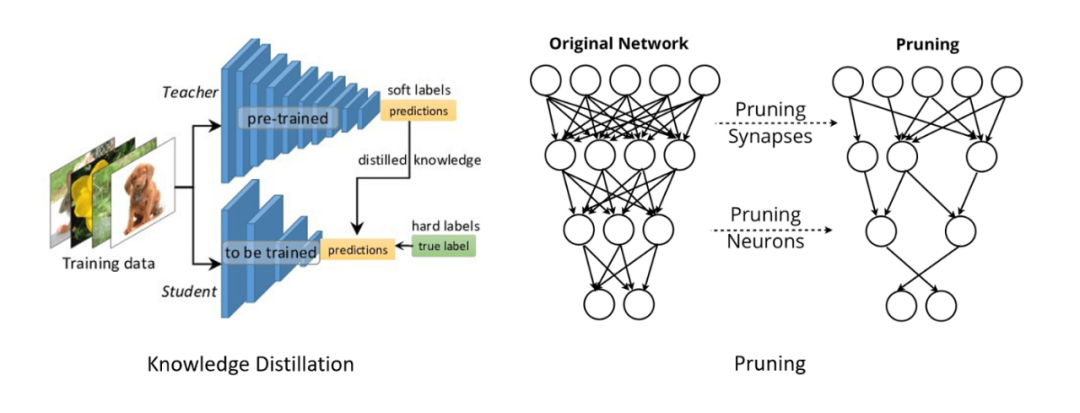
两种流行的近似优化方法。

在最近流行的几种近似优化中，知识蒸馏和剪枝是两种有代表性的方法（如上图所示）。前者尝试使用大型教师网络来更好地训练学生网络；后者则删除了网络中影响较小的权重和激活函数。本文将重点介绍另外一种方法——二值神经网络，这种网络在泛化性能、加速潜力、内存压缩等方面都有优秀的表现。

二值网络

为了提高性能并减少内存需求，研究团队在部署模型时越来越多地量化激活函数和权重。例如，在推理过程中，工程师可能将模型转换为能够对 int8（8 位整数）进行运算的方式，而不是在训练过程中经常使用的 float32（IEEE 754 单精度浮点数）。小型整数运算不仅比浮点运算速度快，更因为它们占用的位数更少，所以可以通过充分利用可用内存带宽来提高吞吐量。在实践中，很多模型被量化后都不会有显著的准确度损失，因此这项技术大受欢迎。

二值化（binarization）将量化进行到了极致，将网络的权重和激活函数降低到只剩一位，这会带来一些新的优化。考虑两个 1 位值之间所有可能的乘法（如下图），这类方程式和「与门」的逻辑真值表极为相似。

如果认为值为 0 的位代表-1，则上表将成为「同或门」的真值表。

这种等效可以让我们用更高效的二值运算代替浮点运算。

浮点点积（上）和二值点积（下）的比较。

对上图点积内循环中的运算次数进行统计可以发现，二值化可以将一层中的运算次数减少到原来的 1/43，将参数大小减少至 1/32。当这样大体量的优化效果首次由 Courbarioux 等人提出时，2016 年便掀起了二值网络研究的热潮。当然，用 1 位值近似 32 位浮点数是一种有损近似。与对应的全精度相比，二值网络通常会有明显的精度损失，top-1 准确率通常会损失近 20％。因此，二值网络的研究重点一直聚焦于如何减少精度损失。

尽管多个研究团队在提高二值网络准确率方面取得了巨大进步，但他们都没有以一种可以衡量端到端加速的方式实现该网络。这种实现的缺乏不仅让我们很难知道二值网络的实际速度，而且还阻止了二值网络在许多实际环境中的应用。

而缺乏实现的原因是，要编写一个简单的二值矩阵乘法，尽管运算次数比较少，但它依然会比大多数的全精度乘法慢得多。函数的运行时间并不完全取决于其运行次数，内存的访问方式也起着重要作用。任何二值网络的实现都必须与 OpenBLAS 和 MKLDNN 这样的库竞争，而这些库经历了大型工程团队多年的手工优化，难度可行而知。而对于大多数研究机构来说，花大量的时间和精力来建立具有竞争力的库根本不可能。取而代之的是，他们在训练期间模拟二值化，并假设根据运算次数可以预测加速。

Riptide 的突围

为了解决这些问题，OctoML 的研究者提出了 Riptide，这是一种找出并解决端到端二值网络瓶颈的方法。Riptide 基于 TVM，后者是一种深度学习系统编译器，可以帮助我们自动生成经过调优的高性能二值化算子。

迄今为止，二值网络优化仅仅着眼于高效实现核心低位（low-bit）卷积层的不同策略。这一着眼点基于以下假设，即二值网络性能可以反映高精度网络的行为：如果核心卷积可以利用尽可能少的位数实现足够高的准确率，那么整个网络将变得非常快。然而，没有哪个二值网络是单纯地由卷积构成。在卷积之间有许多关键的中间运算，需要用它们来处理下一层的数据。在高精度网络中，这些层的延迟可以忽略不计，但在二值网络中，卷积可以实现 43 倍的加速，这些中间「粘合层（glue layers）」就变得非常重要。

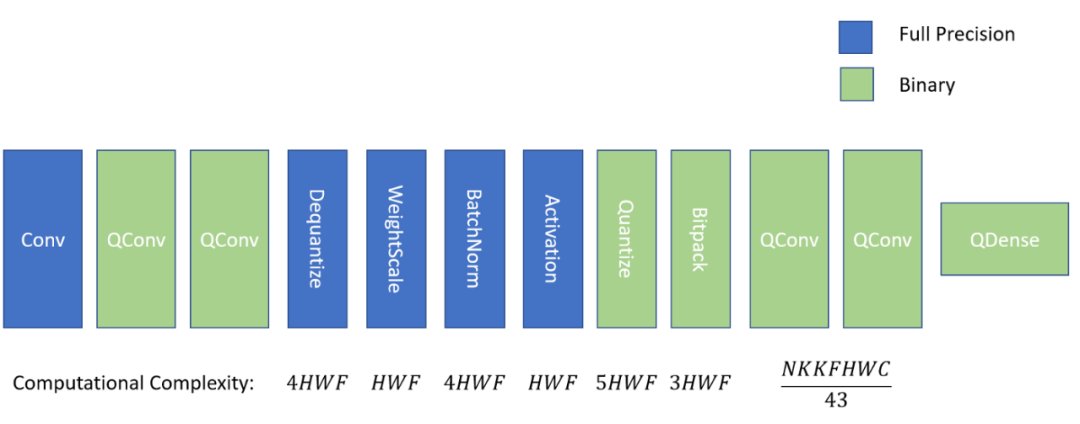
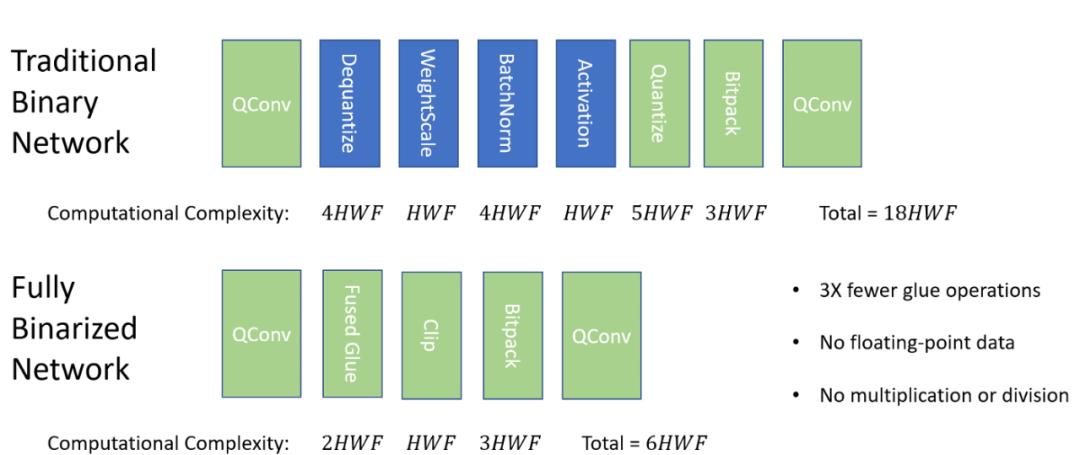
二值卷积之间的「粘合层」及其计算复杂度。H 和 W 表示输入维度，F 表示滤波器的数量。

当前多数的二值网络至少包含 4 个上图中的蓝色层（QConv 和 Quantize 之间）。从左到右来看，首先将 QConv 的输出从整数形式去量化为等效的浮点数，接下来，使用权重缩放（传播实值权重的大小）和批归一化（保持激活的分布可预测）进行缩放。然后应用 ReLU 等非线性激活函数，结果被重新量化为单个位，并打包为下一个量化卷积做准备。

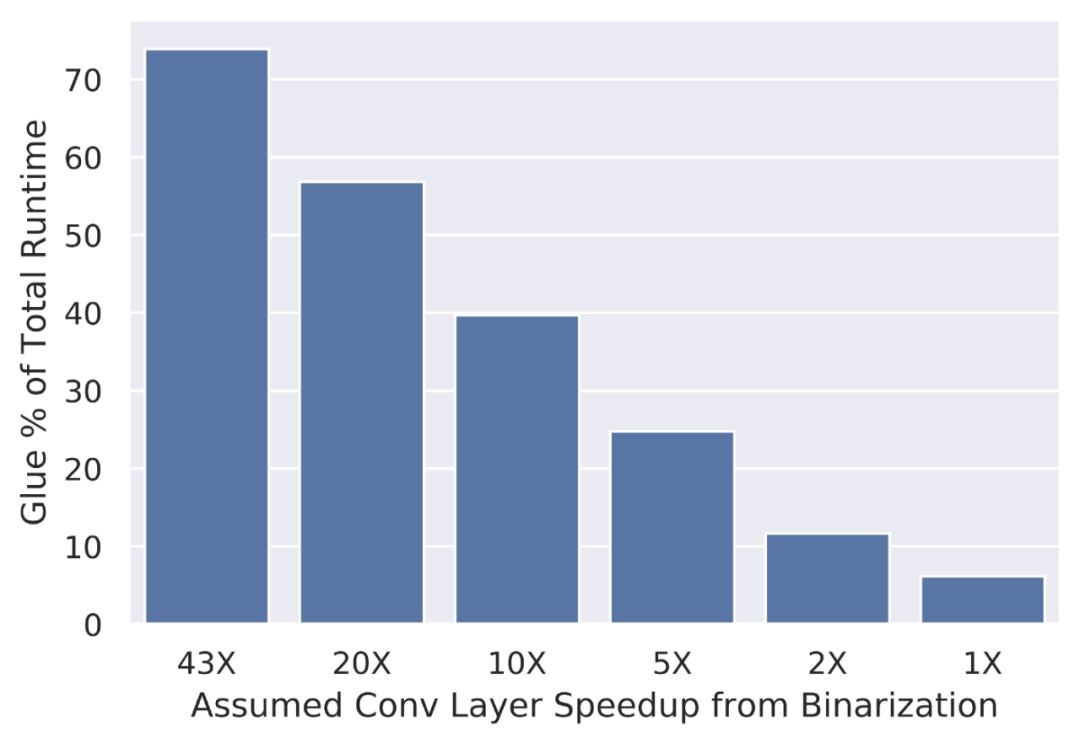
为了理解粘合层的重要性，可以联想一下 SqueezeNet（一种更高效的移动端部署架构）。假设典型的输入大小约为 200x200 像素，并且二值卷积的完美 roofline 实现运行速度是全精度的 43 倍，那么可以估计出网络在粘合层中花费的总执行时间。

假设二值化可以使卷积的速度提高近 43 倍，可以进一步估计，更高精度的粘合层将消耗大约 70% 的总推理时间。这是一个相当大的瓶颈！即使在较低的卷积速度（如 20 倍和 10 倍），粘合层仍然会消耗大约一半的推理时间。因此，研究者认为，要真正实现二值网络所承诺的加速，粘合层也必须是二值化的!

前面已经介绍过融合粘合运算（fused glue operation），它只用两个指令就完全替代了粘合层。细节可以参见论文。其关键思想是用移位运算代替乘法，将缩放项近似为 2 的近似幂，用定点量化近似（fixed point quantized approximations）代替浮点加法和减法。定点量化近似可以直接添加到二值卷积输出中。综上所述，得到如下方程组：

其中，N 是用来量化网络激活的位数，最后一行求解 q(a) 给出了融合粘合的完整方程。通过替换这种融合粘合运算，可以创建一个完全二值化的网络：

研究者还在 ImageNet 数据集上进行了广泛的准确度扫描，发现与其他 SOTA 二值网络相比，上文中的融合粘合运算不会造成任何准确度损失。

这是一个好消息，因为在体系架构层次上消除了粘合瓶颈之后，现在已经可以着手生成快速的二值卷积并度量端到端性能。

端到端加速

早期，研究者将二值网络作为一种近似技术，帮助我们在移动和 IoT 设备上部署高效的模型。先来看一下 Riptide 在树莓派 3b 上的表现如何。树莓派 3b 基于 ARM Cortex-A53 处理器，是资源受限环境的二值目标的典型代表。

首先，将基于 for 循环的简单网络实现与使用 MKLDNN 来加速其浮点运算的完整精度基线进行比较。

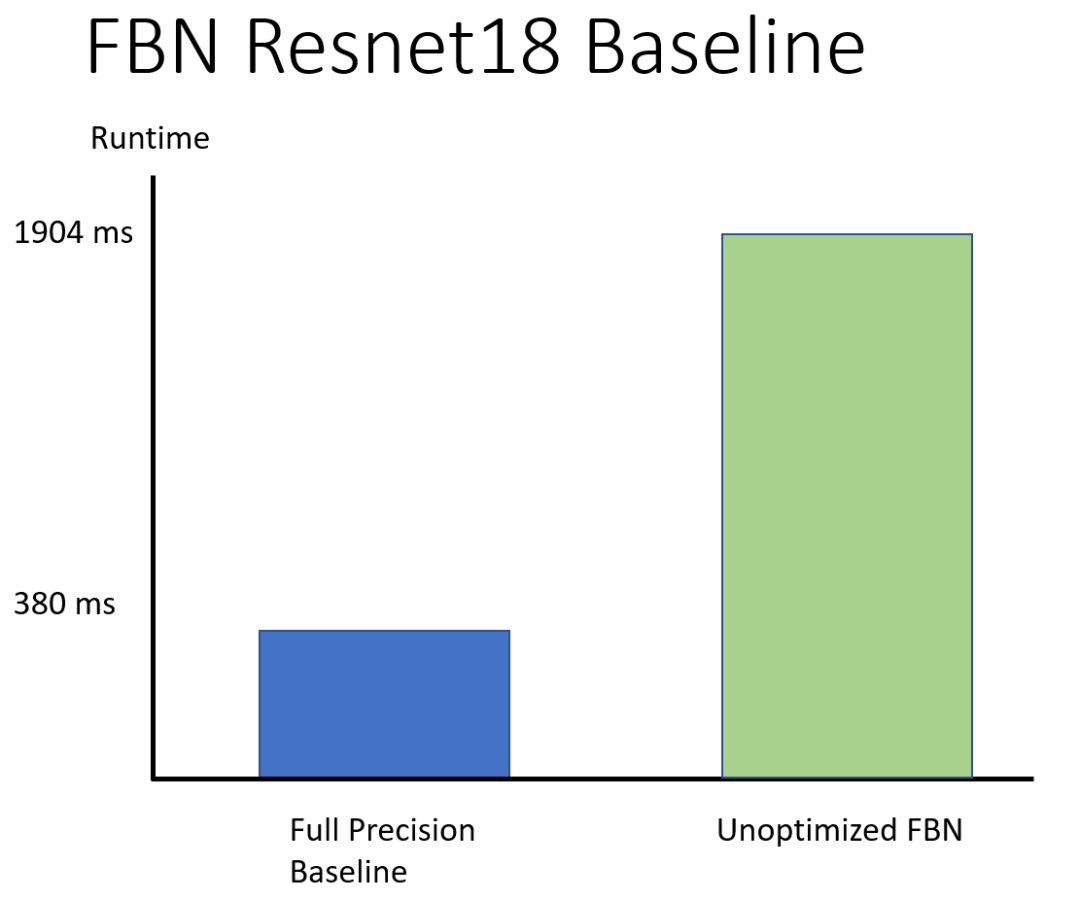
使用 MKLDNN 的完整精度 ResNet18 运行时间 vs. 未优化的完全二值网络。

在没有优化的情况下，研究者获得了 ResNet18 的一个完全二值网络（FBN）版本，其速度大约相当于对应高精度网络的 1/5。为了真正利用二值网络，现在还需要生成一个经过调优的执行 schedule。研究者通过在 TVM 中实现二值算子并利用其强大的调度、优化能力来得到这种 schedule。

TVM 提供了以下可以用于优化函数的 schedule 特性:

• Tiling 将一个计算分解成多个块，以改善负载的内存局部性。

• Vectorization 利用硬件 SIMD 指令来实现更高效的运算执行。

• Parallelization 利用多核等 MIMD 设施。

• Loop Unrolling 复制循环体来减少开销。

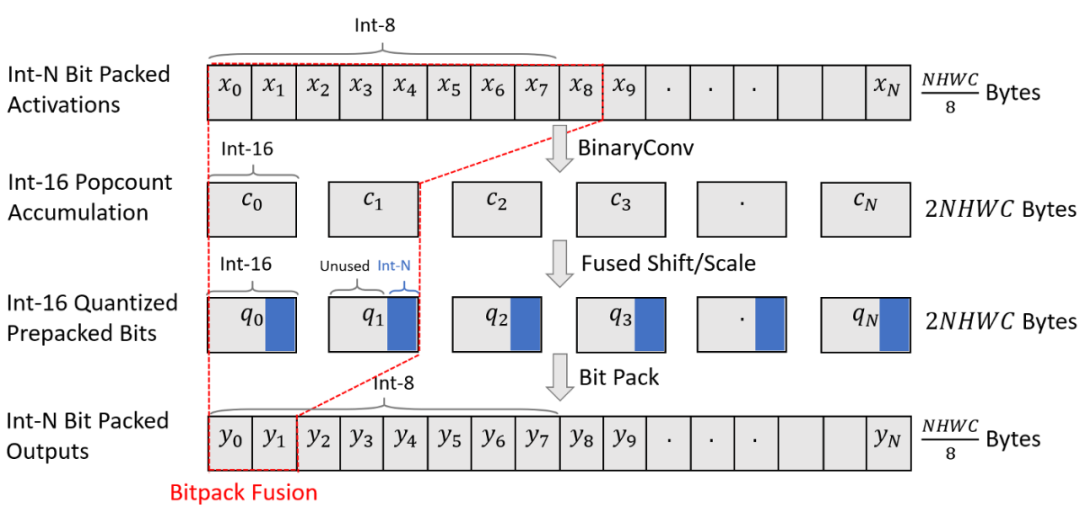
此外，研究者还利用了《Automating Generation of Low Precision Deep Learning Operators》论文中提到的 fast popcount 算子。最后，他们还介绍了一种名为 bitpack fusion 的新优化方法。

Bitpack fusion 将 bitpacking 折叠成卷积，以减少激活内存消耗。

在高级层次上，bitpack fusion 尽可能将 bitpacking 折叠到前面的卷积核中。这可以将中间内存需求减少到原来的 1/16，使得复制策略更加高效，从而提供进一步的加速。

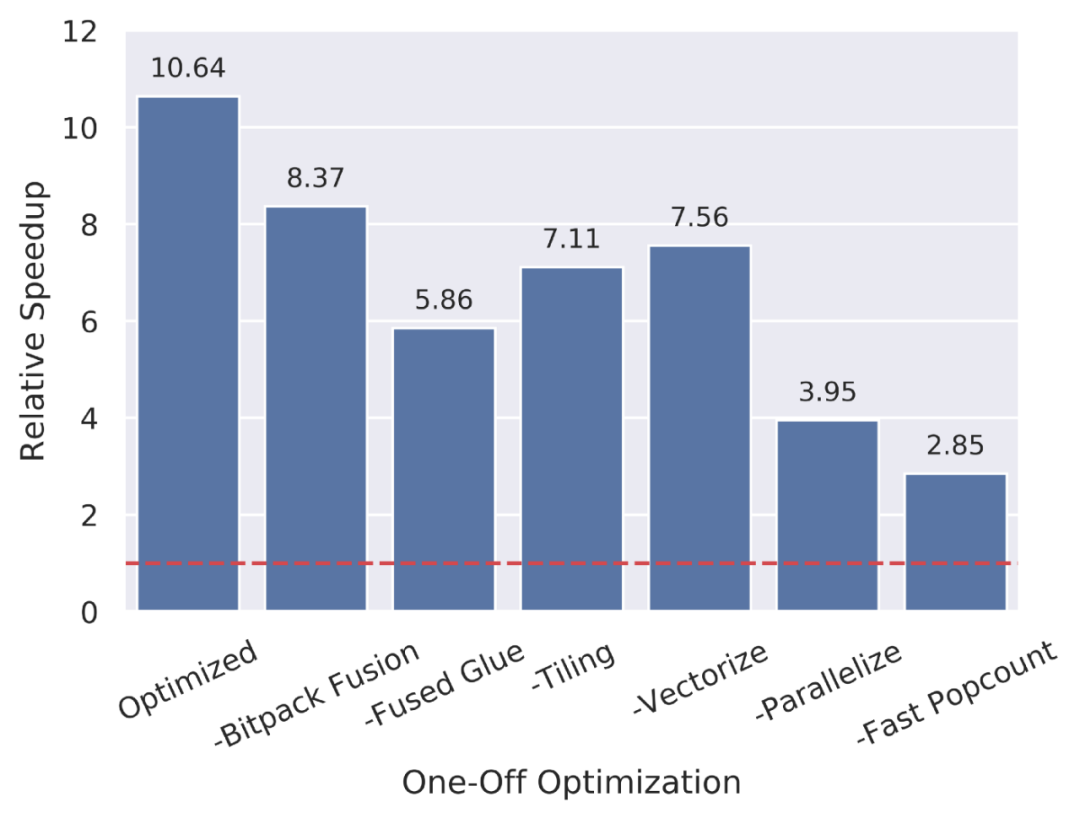
那么，这一堆优化究竟哪些更重要呢？

为了解答这一问题，研究者在 SqueezeNet 上进行了控制变量研究，结果如上图所示。

他们发现，与更高精度的浮点基线相比，每种优化都对加速有显著影响。如果将各种优化方法一起应用，可以在真实模型上看到 10 倍的加速。虽然 10 倍的加速远小于论文中所期望的 43 倍加速，但这也是一个数量级的提升，可以显著扩展能够高效运行 SOTA 模型的设备范围。当然，这种加速只有在保证准确率的前提下才有价值。

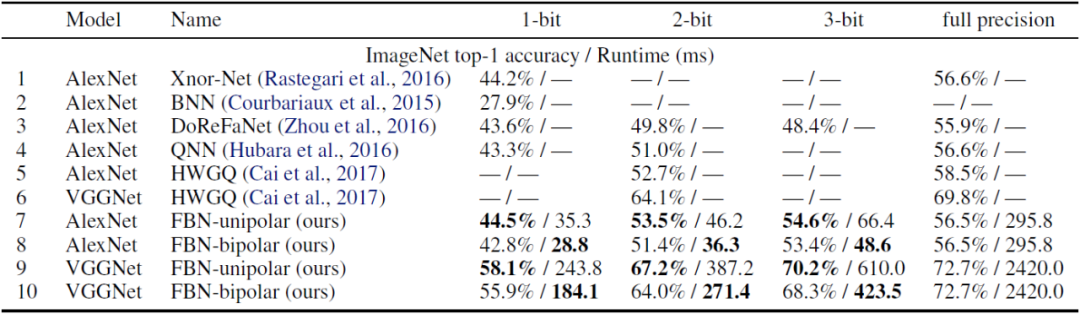
上表显示了几种流行二值模型在 1、2、3 位激活条件下的准确率与运行时间权衡。总体来看，可以发现在提供更多加速的同时，Riptide FBN 和其他 SOTA 二值技术一样稳定，甚至比后者更加准确。Riptide FBN 可以提供准确的激活位宽和量化极性（quantization polarity），提供 4~12 倍的加速，使得它很容易满足所有应用的准确性需求。

原文链接：https://medium.com/octoml/riptide-fast-full-binarization-in-tvm-ae2afd2104bb

作者：Josh Fromm
机器之心编译
机器之心编辑部