看图聊算法:快速排序的原理与实现
在排序的算法中,1945 年由冯·诺依曼发明的归并排序(Merge Sort),是一种典型利用分治策略高效解决问题的算法。
看图聊算法:归并排序的原理与优化
然而,归并排序的缺陷在于其需要额外存储空间。这引发了一个问题:能不能有一种算法,既不依赖额外空间,又能利用分治思想进行原地排序?
快速排序正是这样一种算法。不同于归并排序,快速排序将重心放在“分”上,让“治”自然发生。
快速排序的核心原理
快速排序分为两个核心过程组成:
划分(Partition):选择数组中的一个元素为支点(pivot),通过一次遍历,将小于等于支点的元素移到左侧,大于支点的元素移动到右侧。递归(Recursion):对左右两侧的子数组,重复执行上述操作,直到整个数组完全有序。
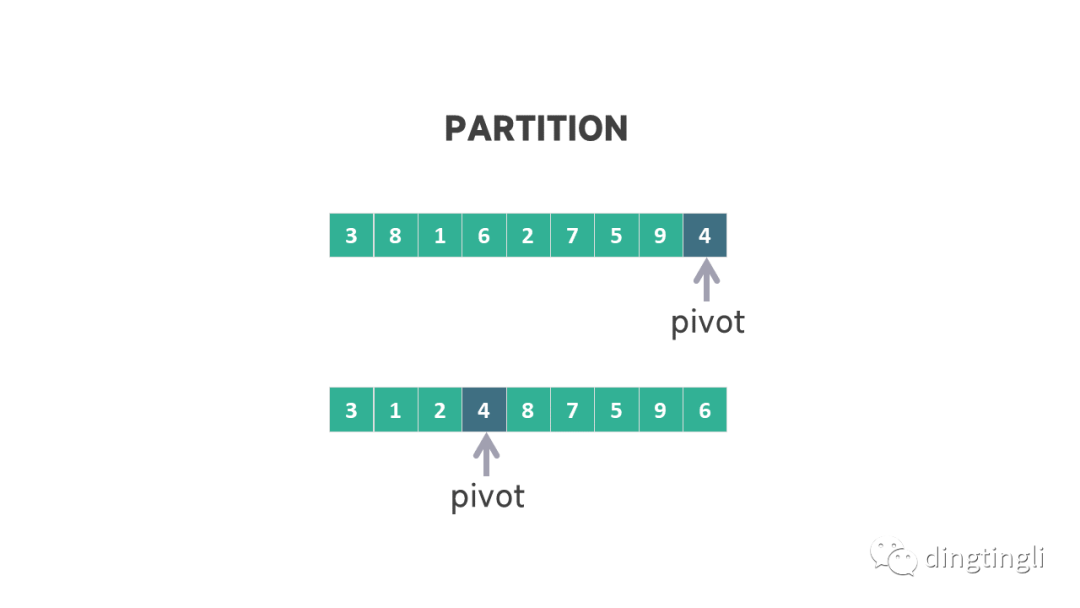
选择合适的支点(pivot)
我们首先来选择支点(pivot),支点的选择对快速排序的效率影响显著。
理想情况下,支点选择数组中位数,这样能确保划分后的子数组尽量平衡,从而最大限度地发挥分治的效果。
但在实际操作中,每次都去找中位数从性能上看,似乎划不来。因此,对于随机排列的数组,直接选择最后一个元素作为支点,不失为一种好方法。
划分(Partition)过程
选择好支点后,我们可以对数组进行划分操作,将小于等于支点的元素移到左侧,大于支点的元素移动到右侧。这也是快速排序算法中最重要的部分。
划分
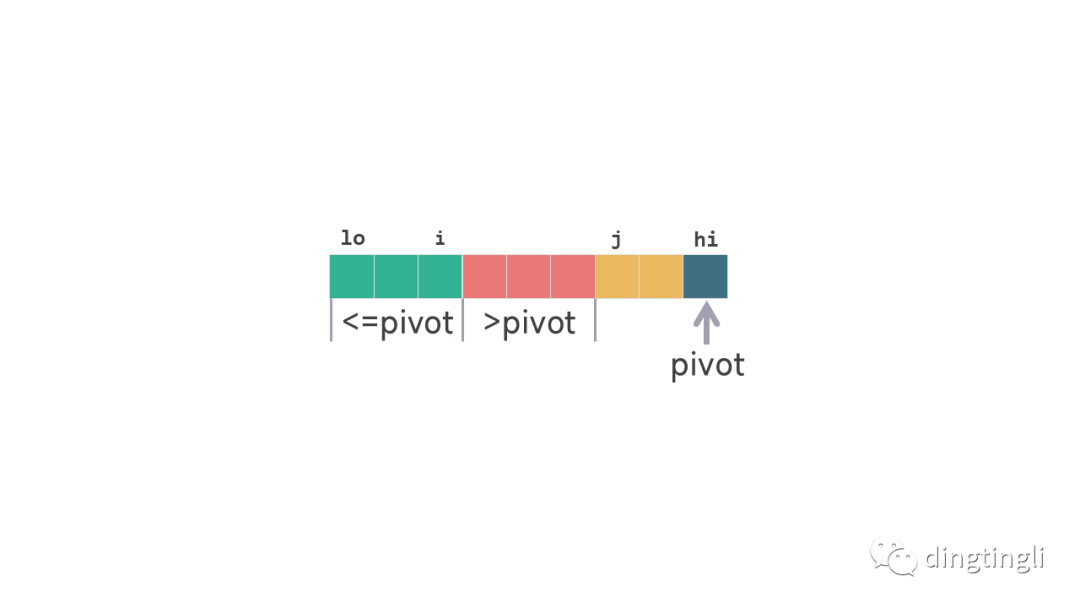
在这一过程中,通过一次数组扫描并设置两个指针 i 和 j,确保在扫描过程中满足以下条件:
- [lo, i] 之间的元素都
<=pivot。 - [i+1, j-1] 之间的元素都
>pivot。 - [j, hi-1] 之间的元素未被扫描。
划分扫描条件
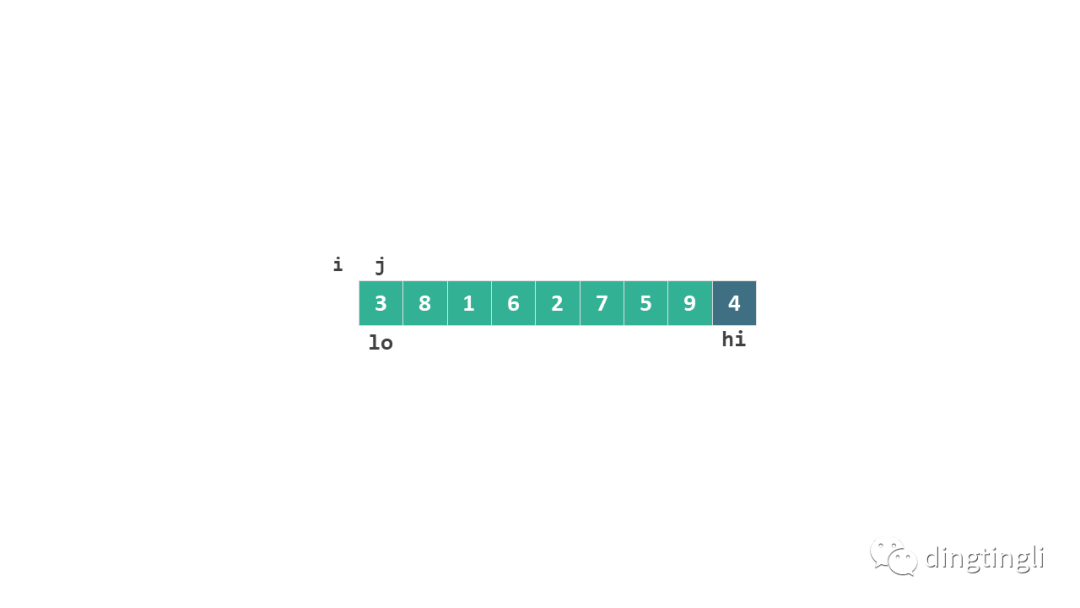
扫描初始化:在扫描开始前,我们设置 i=lo-1 和 j=lo以保持上述三个条件成立。
这样,在初始状态下 [j, hi-1] 之间是所有未扫描的元素,[lo, i] (<=pivot) 和 [i+1, j-1] (>pivot) 的区间都不存在。
划分扫描初始化扫描过程:
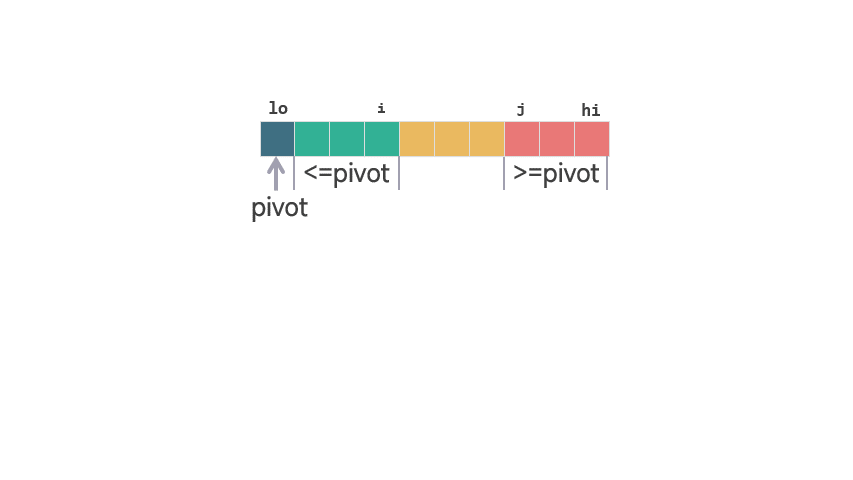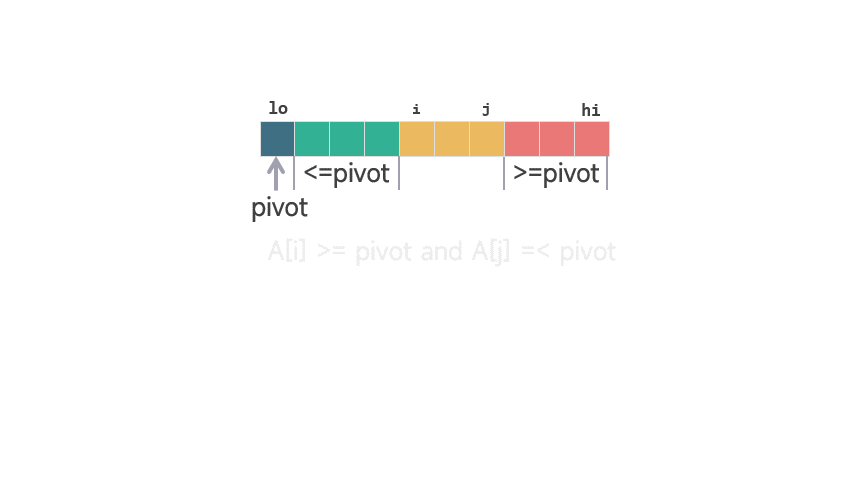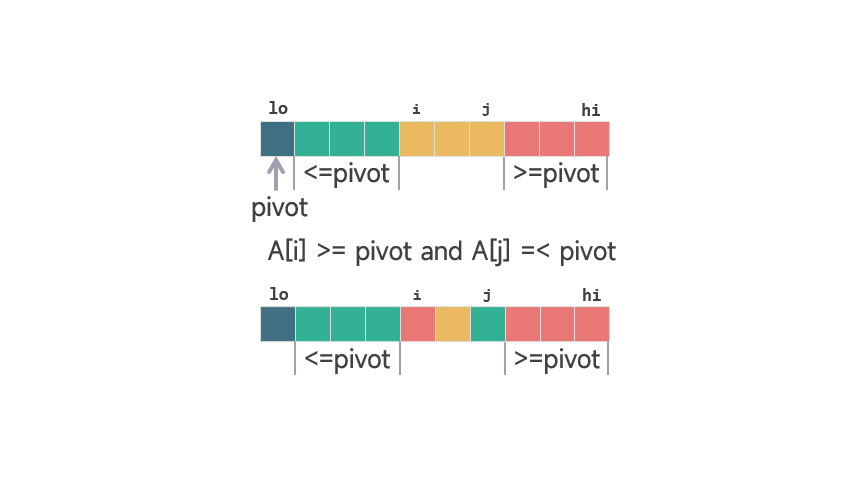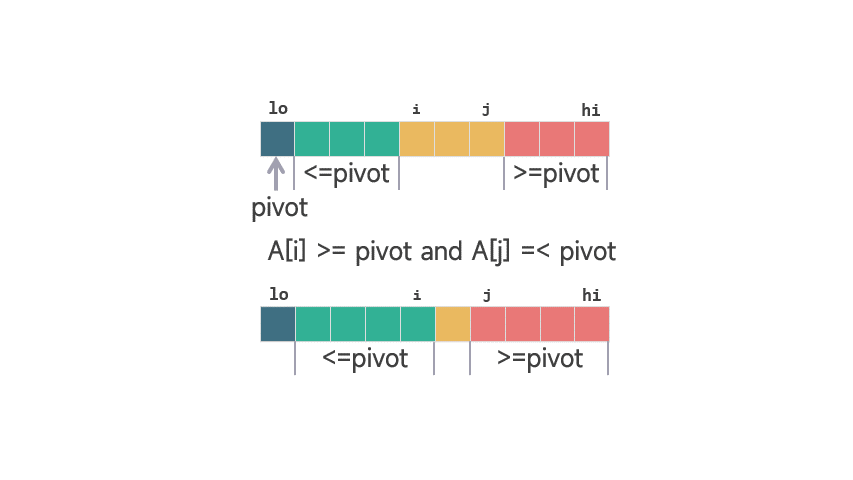
当 A[j] > pivot 时,j 的值加 1。保证 [i+1, j-1] 之间的元素 >piovt。
动图 划分扫描过程 1当 A[j] <= pivot 时,i 加 1,交换 A[i] 和 A[j] 的值之后,j 再加 1。这样同时保证了 [lo, i] 之间的元素 <=pivot,并且 [i+1, j-1] 之间的元素 >piovt。
动图 划分扫描过程
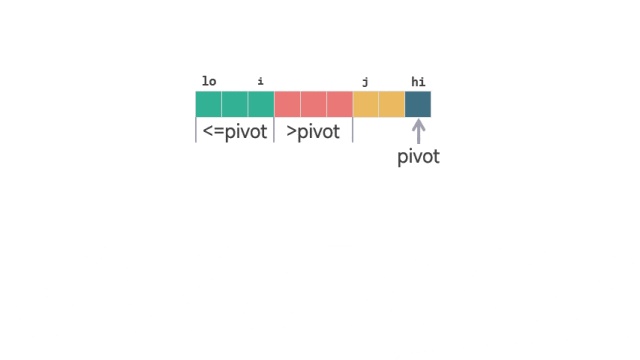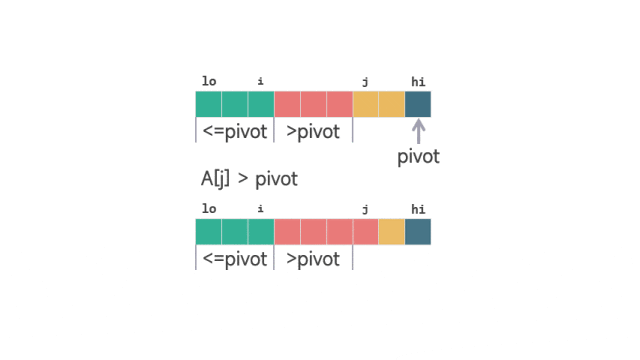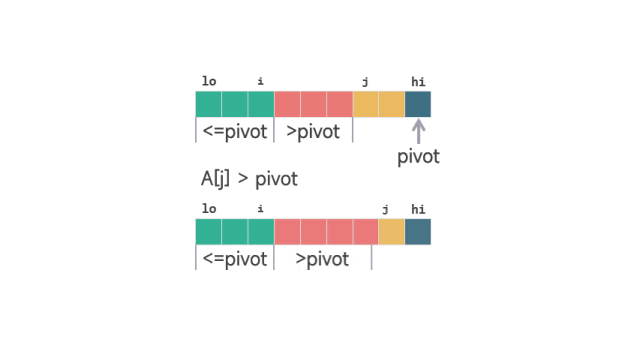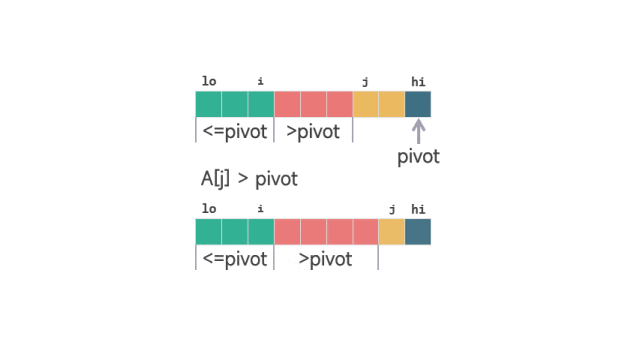
2扫描结束:扫描完成时,j = hi,此时我们需要将支点 A[hi] 置于正确位置。通过交换 A[hi] 与 A[i+1],支点就位,返回其索引。
动图 划分扫描结束
将上述的扫描过程转化为代码是一个有趣的挑战,你可以先思考一下如何实现。这里提供一个我编写的函数,以供参考:
def partition(A, lo, hi):
pivot = A[hi]
i = lo - 1
for j in range(lo, hi):
if A[j] <= pivot :
i = i + 1
A[i], A[j] = A[j], A[i]
A[i + 1], A[hi] = A[hi], A[i + 1]
return i + 1视频 划分扫描执行过程
注意:你可以在我的 github 仓库中查看源代码
https://github.com/dingtingli/algorithm/blob/main/Code/quicksort01.py
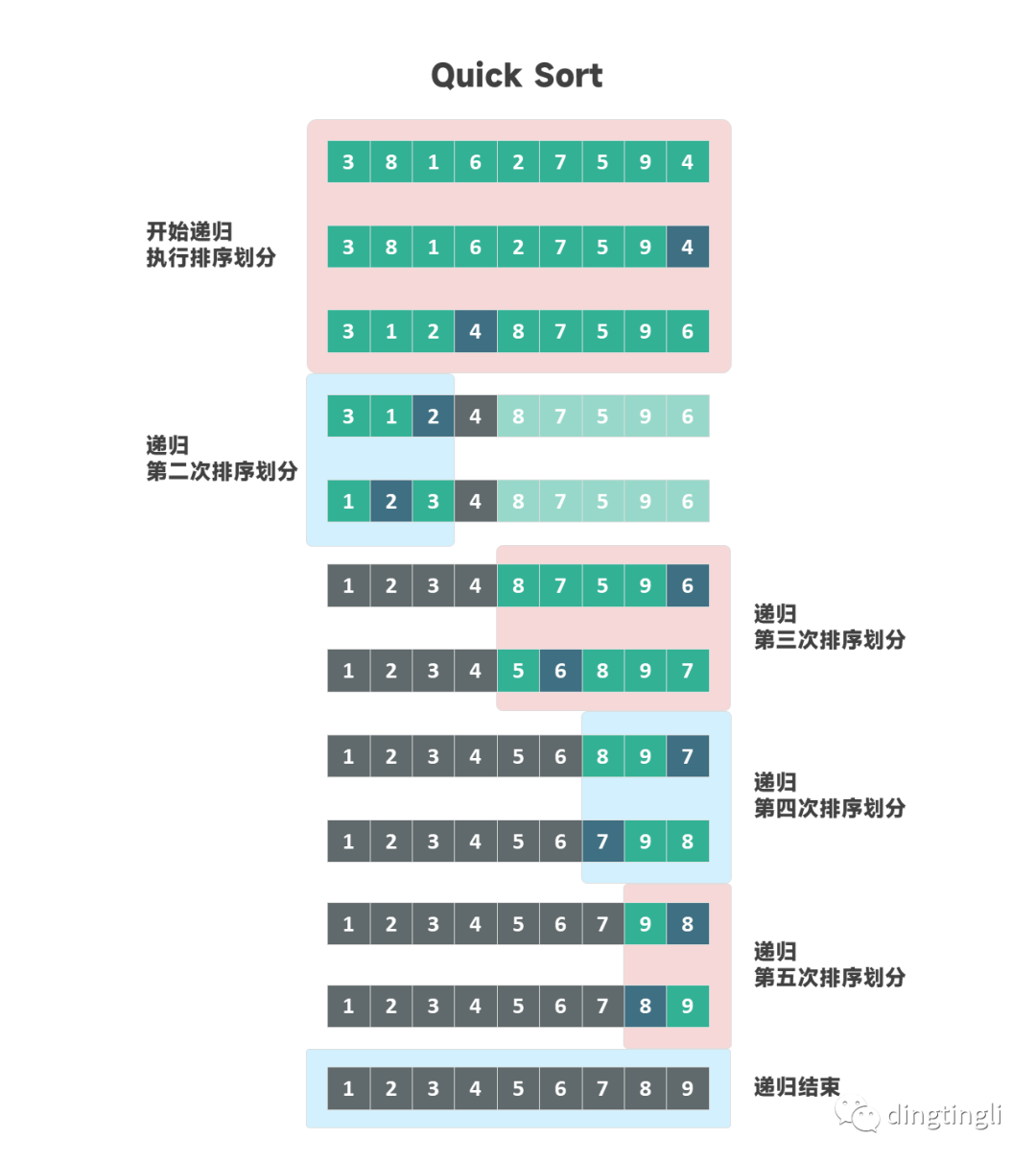
递归:实现快速排序
我们来完成最后一步,通过递归不断地对子数组进行划分,直到每个子数组只有一个元素,整个数组就被排序完成。
def quicksort(A, lo, hi):
if lo < hi:
pivot_index = partition(A, lo, hi)
quicksort(A, lo, pivot_index - 1)
quicksort(A, pivot_index + 1, hi)详细的递归执行过程示意图如下:
递归执行示意图
*注意:你可以在我的 github 仓库中查看源代码*https://github.com/dingtingli/algorithm/blob/main/Code/quicksort01.py
双指针遍历
在划分过程中,我们采用了双指针技术,这是一种常见的算法策略。该技巧有以下常见步骤和策略:
- 确定指针的移动策略:确定如何移动两个指针以达到目的。
- 计算和更新结构:使用两个指针计算结果,并根据需要更新结果。
- 处理边界和特殊情况:考虑两个指针到达数组边界时的情况。
双指针技术不仅用于快速排序,还广泛应用于其他算法和问题,例如:在有序数组中查找特定和的两个数;计算数组的最大/最小子数组和;检测链表中是否存在环。你可以思考一下:是否还有其它双指针移动策略来实现快速排序中的划分过程?
我们将在下一篇文章中优化现有的快速排序,其中将会使用新的双指针移动策略,如果有兴趣,请关注更新吧。
动图 双指针遍历